Semstem
Semstem is a method for the inference of stemmatological trees. Its origins go back to the Bayesian Structural Expectation-Maximalization algorithm (SEM, see Friedman 1998). This SEM algorithm uses maximum likelihood estimates to compute expectations and maximalisations for missing data. Semstem, proposed by Teemu Roos and Yuan Zou in 2011 (see Roos & Zou 2011), is an extension and adaptation of Semphy, an earlier phylogenetic method implementing SEM (see Friedman et al. 2002). The Semstem algorithm is aimed at uncovering latent tree structures – i.e. proposing likely stemmata. Semstem differs from other algorithms in that it is not limited to producing bifurcating trees, and that the degree (the number of incoming and/or outgoing edges) of the internal nodes is not limited either. Also the extant manuscripts used as input to the method can be used as labels for the internal nodes as well as the leaf nodes of the stemma. These aspects arguably make the results easier to interpret. The figure below illustrates these points.
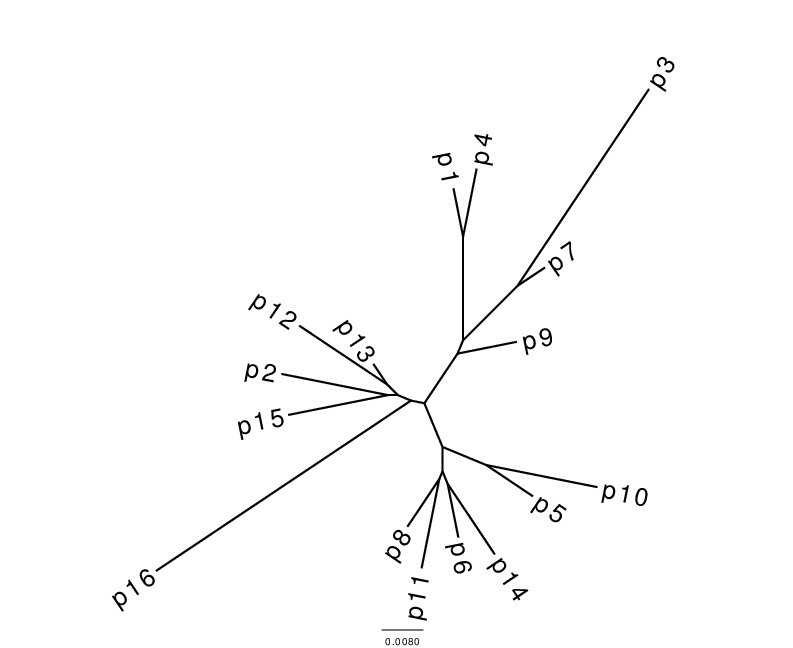
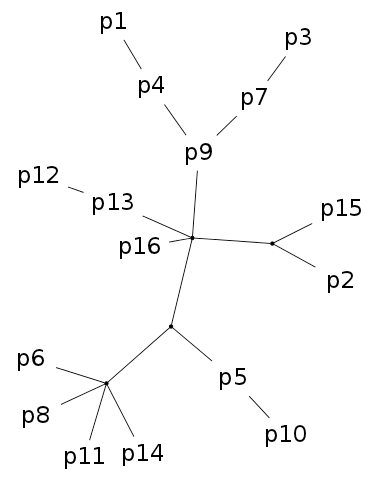
Fig. 1. Stemmata obtained from the artificial textual tradition Parzival. The Neighbour joining (NJ) tree on the left is, as always, bifurcating and all taxa are placed at leaf nodes. In the Semstem tree on the right, there are multifurcations and some of the taxa, for example p9, p7 and p4, are placed at internal nodes. The edge lengths in the Semstem result are arbitrary and chosen to best display the tree structure.
The base algorithm (SEM) infers the unknown contents of latent (or unobserved) nodes—nodes not having been considered by the algorithm for computing a previous tree structure—based on the contents of observed nodes. This additional (estimated) knowledge is then used to derive a maximum likelihood tree, the process for which again will feature a number of unobserved nodes. The algorithm iterates this process the produce a best estimate tree structure. User input is required to determine the total number of iterations before the algorithm terminates and outputs the so far best tree structure.
References
– Friedman, Nir. 1998. “The Bayesian Structural EM Algorithm.” In Uncertainty in Artificial Intelligence: Proceedings of the Fourteenth Conference (1998), edited by Gregory F. Cooper, 129–138. San Francisco: Morgan Kaufmann. Available at: www.cs.huji.ac.il/~nir/Papers/Fr2.pdf Accessed 28 October 2015.
– Friedman, Nir, Matan Ninio, Izsik Pe’er, and Tal Pupko. 2002. “A Structural EM Algorithm for Phylogenetic Inference.” Journal of Computational Biology 9 (2): 331–353.
– Roos, Teemu, and Yuan Zou. 2011. “Analysis of Textual Variation by Latent Tree Structures.” In Proceedings of the 11th International Conference on Data Mining (ICDM-2011), edited by Diane J. Cook, 567–576. Los Alamitos, California: IEEE Computer Society. Available at: http://www.cs.helsinki.fi/u/ttonteri/pub/icdm2011.pdf. Accessed 28 October 2015.