Complex dynamics, spring 2017
Complex dynamics, spring 2017
News
Today, May 3, the last lecture.
If you need tutorial for your essay, you can contact Kari Astala by email (kari.astala@helsinki.fi), or see Lauri Hitruhin in person (room C414; his email: lauri.hitruhin@helsinki.fi).
The essay should be returned by May 20, to: kari.astala@helsinki.fi
Results of the course exam (on the first part of course) can be found on "Koetulokset / Exam results" -webpage. Average of exam was 18,6 / 24.
Essays
are some suggestions for topics for an essay, to pass the second part of the course..
Team-work is also possible for essays; some of the topics can easily be adjusted for this.
The essay should be roughly about 5-8 pages, depending on the case of course. Naturally, for team works the length should be roughly adjusted by the "team size".
The essay should be returned by May 20, to: kari.astala@helsinki.fi
Teacher: Kari Astala
Scope: 10 cr
Type: Advanced studies
Teaching: On Mondays and Wednesdays, at 12 - 14 in room C123. First lecture Monday 16.1.2017
Topics: Complex dynamics (i.e. holomorphic dynamics) belongs to two fields, 'Dynamical Systems' and 'Complex Analysis'. In complex dynamics one studies the discrete-time dynamical system of iterating a complex polynomial P(z). That is, setting zn+1 = P(zn), n = 0, 1, 2,... , one wants to understand the asymptotic behaviour of zn, when n → infinity, and see e.g. how this depends on the initial value z0. Typical questions are for instance the geometric properties of the associated attractor or of the chaotic part of the system (the Julia set).
Compared to other dynamical systems, in complex dynamics it is possible to achieve, with tools from complex analysis, a surprisingly detailed understanding of the systems. For complex analysis, complex dynamics allows fascinating applications of the methods and results of the field.
In brief, the aim of the course is to understand these questions, both local dynamics and, in particular, the geometry of Julia sets and the Mandelbrot set.

One can study also dynamics under a rational function R(z) or an entire function f(z). If time allows some topics of these will also be discussed.
Prerequisites: The starting point is knowledge of basic complex analysis, e.g. as covered in the course 'Complex Analysis I'.
More material and additional results from complex analysis will be necessary, but these will be covered during the course.
Thus one may think the course also as a replacement or an alternative for the course 'Complex Analysis II'
Teaching schedule
Weeks 3-9 and 11-18, Monday and Wednesday 12-14 in room C123.
Easter holiday 13.-19.4.
In the first period, weeks 3-9, there will be exercises every week (for details on these see below).
Exams
The exam for the first part of the course is on Tuesday March 14, at 10.15 - 12.45, room DK117.
The area of the exam is Chapters 1-5 of the course notes.
For the second part, the grade is obtained by writing a short essay.
Course material
HERE you have the first seven chapters of the course notes plus half of Chapter 8, including lectures of April 26.
The proof of theorem 7.38 is still missing.
There are several books on this topic; for instance
- Beardon, Iteration of Rational Functions, Springer-Verlag
- Carlson-Gamelin, Complex Dynamics, Springer-Verlag
- Berteloot - Mayer, Rudiments de Dynamique Holomorphe, Lecture notes (In French)
From the following addresses you can get programs to draw Julia sets (Hints by Jan Leino and Valter Uotila):
- Download "XAOS" from http://fractalfoundation.org/resources/fractal-software/
- Download "Visualisoija" from https://www.cs.helsinki.fi/u/jllang/visualoija/
- http://www.mndynamics.com/indexp.html.
Did you forget to register? What to do?
Exercises
Exercises are can be found on this page every Wednesday, and exercise classes are on the following Tuesday, at 10-12, room C129.
Exercise classes are given by Lauri Hitruhin. First exercises Tu 24.1.
Based on the number of exercises done you get extra points as follows:
25% = +1p, 35% = +2p, 45% = +3p, 55% = +4p, 65% = +5p ja 75% = +6p.
Assignments
- Exercises 1 Solutions 1
- Exercises 2 Solutions 2
- Exercises 3 Solutions 3
- Exercises 4 Solutions 4
- Exercises 5 Solutions 5
- Exercises 6 Solutions 6
Exercise classes
Group | Day | Time | Room | Instructor |
|---|---|---|---|---|
1. | Tu | 10-12 | C129 | Lauri Hitruhin |
Course feedback
Course feedback can be given at any point during the course. Click here.
___________________________________________________________________________________________________________________________________________
Some Pictures:
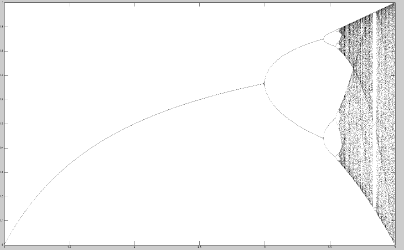
Feigenbaum diagram:
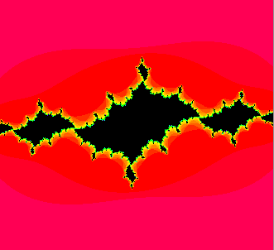
Typical (filled in) Julia sets; Julia set = boundary of the black part; Black = filled in Julia set
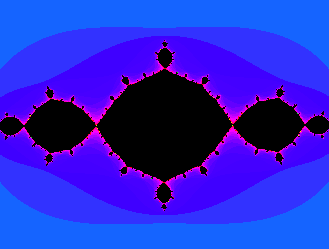

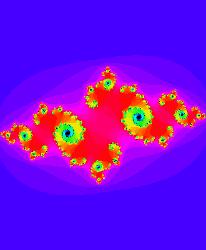

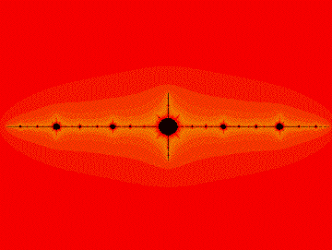
A holomorphic motion of a Julia set.
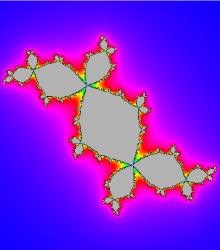

Julia set of P(z) = z2 + i; The critical point is preperiodic.
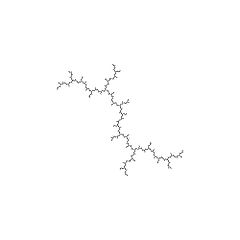
Fatou set with three external rays landing at a same point.
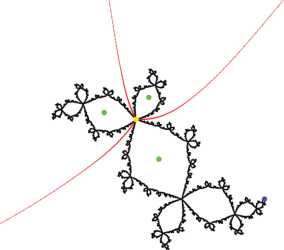
Julia set and its combinatorial description:
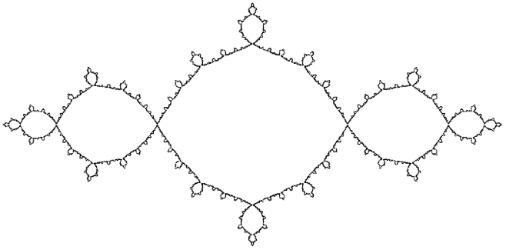
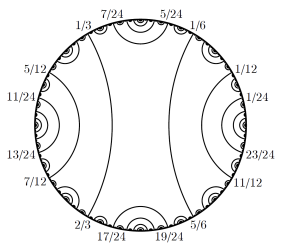
Mandelbrot set:

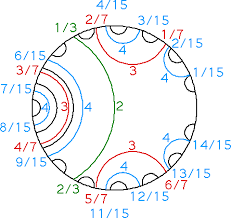
Combinatorial Mandelbrot set :

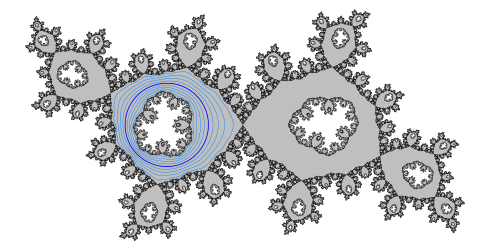
A rational map with a Herman ring
Newton's root finding algorithm for P(z) = z3 - 1:

Quasiself-similarity
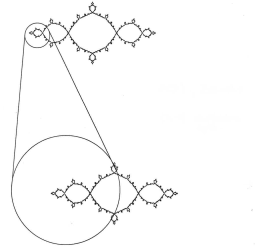
Self-similar sets:
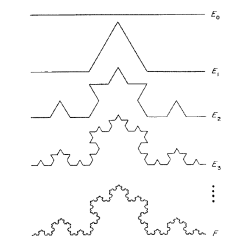
Von Koch snowflake
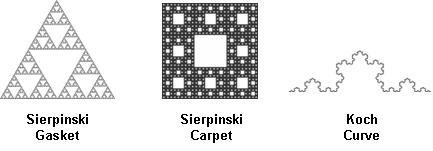
Other self-similar sets

Here is a self-affine set.
