Introduction

Theory

The observational geometry is characterized by four angles: the angle of incidence \(\theta_i\), the angle of emergence \(\theta_e\), the azimuth angle \( \phi\), and the phase angle \(\alpha\) (see figure).

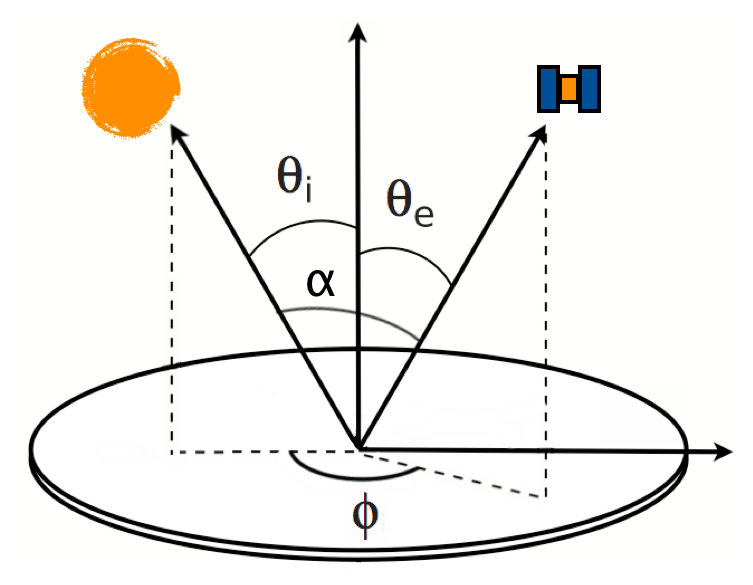
The cosines of incidence and emergence are \( \mu_0 = \cos \theta_i\) and \( \mu = \cos \theta_e\)
 

The relationship between the observed intensity of the light scattered by the surface for incident flux density \(\pi F_0\) can be written

Our scattering model has the form

Surface parameters

The media are characterized by three parameters. The most important is the packing density of the spherical particles, denoted with \(\nu\). The two other parameters describe the roughness of the macroscopic boundary between the medium and space. This boundary is a fractal surface (fractional Brownian motion, fBm). The two parameters describing the fBm surface are \(H\), the fractal Hurst exponent, and \(\sigma\) the amplitude. In general, lower \(\nu\), lower \(H\), and higher \(\sigma\) mean a rougher surface with stronger shadowing effects.

Data files

File structure

The provided data files are in the NetCDF-4 format. The file contains one main variable, the Hemisphere table, which contains the actual scattering model values, as well as a number of "global attributes", which contain metadata, some of which are important.

The files contain the scattering model values, with the incident cosine, and without the phase function and volume-element albedo:

Usage

In what follows the indexing of arrays starts from zero.

The desired hemisphere file must first be read by the program. Libraries for reading NetCDF files exist for all major programming languages. Please consult the documentation of your programming language of choice, or the the official NetCDF documentation for more details on this.

To acquire a scattering model value from the hemisphere file, you need to read the main Hemisphere array, as well as the dTheta value and the dPhi and cIdx arrays from the file.

Given your scattering geometry where theta_i is the incident angle, theta_e is the emergent angle and phi is the azimuth angle, compute:

          i = floor(theta_i / dTheta)
          m = floor(theta_e / dTheta)
          n = floor(phi / dphi[m])
          j = cIdx[m] + n - 1
        

Now, the scattering model value S can be found from the Hemisphere array. The first axis is the hemispherical binning over theta_e and phi, and the second is the binning over incidence angle. Therefore the desired value is found thus:

          value = Hemisphere[j,i]
        

Now, value is the main part of the scattering law, and the final scattering model value for the surface element, with volume-element albedo omega_V and phase function P11 is

          I = omega_V * value * P11(alpha)
        

Data download

The individual data files can be found here. The numbers in the filename specifies the packing density (between 0.15 and 0.55), Hurst exponent (0.20 to 0.80) and roughness amplitude (0.00 to 0.10), in this order.

License

The data files are provided under a Creative Commons Attribution 4.0 International license. The citation to use in an academic publication is Wilkman et al. (2015) Planetary and Space Science 118, doi:10.1016/j.pss.2015.06.004.

The data may contain errors, and the author is not responsible for problems arising from these.

All source code possibly provided on this page (though currently none) is under the MIT license:

          The MIT License (MIT)

          Copyright (c) 2015 Olli Wilkman

          Permission is hereby granted, free of charge, to any person obtaining a copy
          of this software and associated documentation files (the "Software"), to deal
          in the Software without restriction, including without limitation the rights
          to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
          copies of the Software, and to permit persons to whom the Software is
          furnished to do so, subject to the following conditions:

          The above copyright notice and this permission notice shall be included in
          all copies or substantial portions of the Software.

          THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
          IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
          FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
          AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
          LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
          OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
          THE SOFTWARE.